Belts
Intro
hook/description
Concepts
Positioning
Slipping
Power Transfer
Positioning
Relevance: Belts are nifty devices to transport power over long distances. They can be used for reductions like gears but without the counter rotating property or as a conveyor belt to transport items.
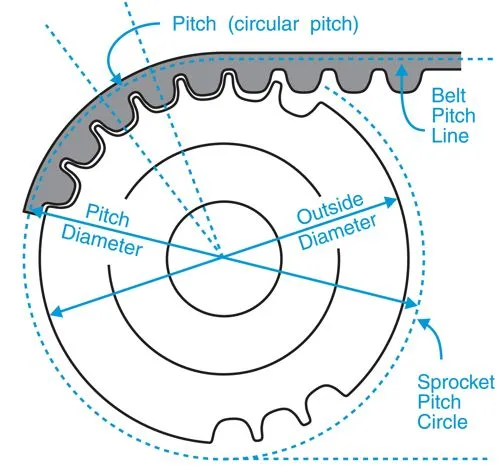
The pitch diameter of a pulley is determined by the equation:
$$D=\frac{p*T}{\pi}$$
Notice that the equation is different form that for gears!
In words, the pitch diameter of the pulley is equal to the pitch of the pulley multiplied by the tooth count and divided by $\pi$.
In comparison with gears, $\pi$ divided by pitch can be seen as an analog to diametral pitch.
Gears:
$$dpD=T$$
Belts:
$$\frac{\pi}{p}D=T$$
Unlike with gears, belts follow a path. Which is probably why the formula is based of off the arc length of the pitch circle (circumference = $\pi D$) than the diameter.
Although the path length can be found by hand this can be time consuming and changes from problem to problem.
I would recommend finding the path length of a custom path using Solidworks. Essentially, the path can be drawn out and dimensioned and then after selecting each part of the path (or fitting a spline) the total length should be reported in the bottom right.
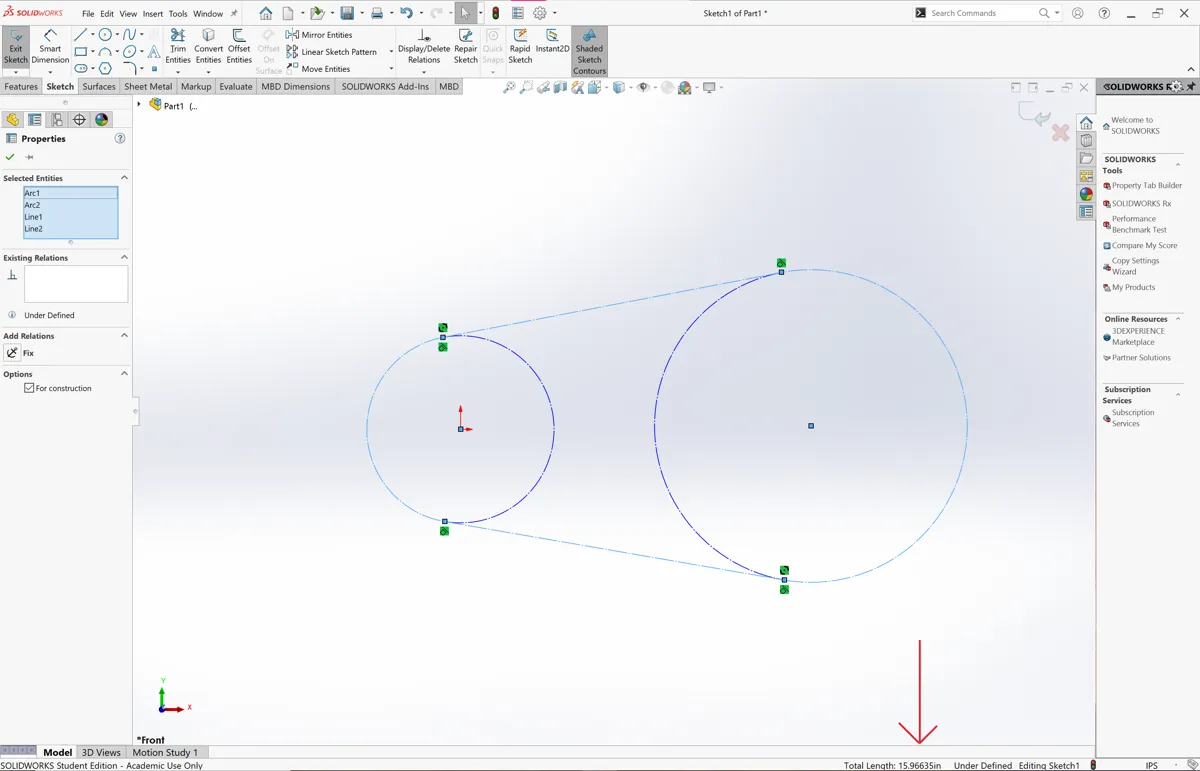
To find the tooth count from the path length, simply divide by the pitch like we did before.
$$\frac{L}{p}=T$$
Special Cases
Equal Sized Pulleys
When a single belt loop is formed by equal sized gears the equation for the path length simplifies.

Note: this derivation was not found mathematically but only visually.
The path length can be calculated by the circumference of one pulley and the distance between the pulleys.
The blue lines are equal to the distance between the centers of the circles. The red curves add up to the circumference of one circle.
$$L=\pi D+\sum_{i=0}^{n}cd_i$$
The path length is equal pi times the pitch diameter of the pulleys plus the sum of all the connecting center distances.
Two Pulleys
For when a belt is connecting different sized pulleys.

$$L=2cd+\frac{\pi}{2}(D+d)+\frac{(D-d)^2}{4cd}$$
An excellent walk-through is given here: