Elevators
Intro
Elevators are an essential part of any FRC toolkit. They facilitate moving game pieces vertically over a large range of motion. If designed to do so, elevators can also act as climbers to help lift the robot up.
Concepts
Relative Motion
Relevance: When designing an elevator, understanding how the stages move relative to each other is essential to choosing the right gearbox to power it.
Elevators generally come in two styles of rigging: continuous and cascaded.

Both can be powered up and down although it may useful to just let gravity or a spring return the elevator. Continuous elevators spool sting on the up run (the motion as the elevator moves up) and the down run (the motion as the elevator moves down) at the same rate. Cascades don’t. The spool for an up run may need to spin at different rate compared to the down run or have a different diameter. Cascades are typically faster than a continuous but they also require more torque. Cascades are made by connecting each stage with a separate piece of string while continuous uses one long piece.
Torque
Relevance: Elevators use gearboxes to move the stages. What follows is the math used to calculate the torque required to move an elevator.
Continuous: TBD
Cascade:
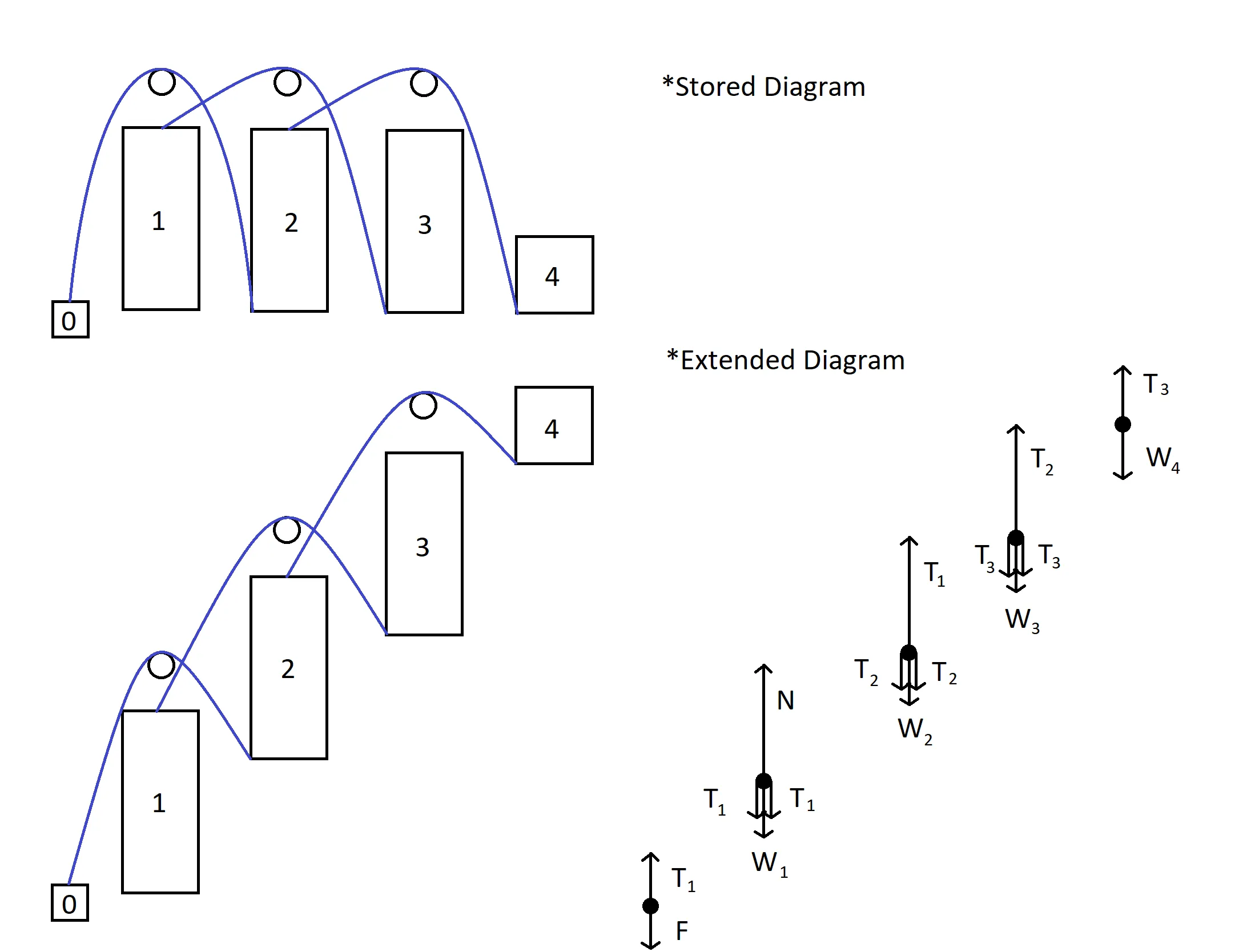
In the image above the numbers refer to “objects.” Object 0 is the force generator: a weight, a gearbox, etc. Objects 1 through 3 are elevator frames and object 4 is the carriage. A three stage elevator is depicted as there are three moving stages.
Assume that friction is negligible, that the string is generally the exact length and is taut, and that up is positive.
First let’s find F assuming static equilibrium.
| Equation | Comment |
|---|---|
| $$F=T_1$$ | Net force eq. for free body 0 |
| $$F=2T_2+W_2$$ | Substitute with free body 2 |
| $$F=2(2T_3+W_3)+W_2$$ | Substitute with free body 3 |
| $$F=2(2W_4+W_3)+W_2$$ | Substitute with free body 4 |
| $$F=4W_4+2W_3+W_2$$ | Distribute |
Generalizing this to n stages we get:
| Equation | Comment |
|---|---|
| $$F=W_2+2W_3+3W_4+4W_5+2^{n-1}W_{n+1}$$ | Nesting multiplicative 2s = power |
Assuming the elevator is accelerating and not in dynamic equilibrium, find an equation for the acceleration of the final stage in terms of the acceleration of object 0 and other variables.
| Equation | Comment |
|---|---|
| $$L_j$$ | Length of the jth object |
| $$\Delta y_j$$ | Change in displacement of the jth object |
| $$\frac{\Delta y_2}{L_1}=\frac{\Delta y_3}{L_2}=\frac{\Delta y_4}{L_3}$$ | Cascade % of previous stage mechanic |
| $$\frac{\Delta y_2}{L_1}$$ | % of stage traveled |
| $$\Delta y_2 = -\Delta y_0$$ | Same string/pulley mechanic |
| $$-\frac{\Delta y_0}{L_1}$$ | % of stage traveled; $\Delta y_0$ is negative |
| $$h=(\frac{\Delta y_0}{L_1})L_1+(\frac{\Delta y_0}{L_1})L_2+(\frac{\Delta y_0}{L_1})L_3$$ | Height from base of Object 1 to base of Object 4 |
| $$h=(\frac{\Delta y_0}{L_1})(L_1+L_2+L_3)$ | Factoring |
| $$h=(\frac{L_1+L_2+L_3}{L_1})(-\Delta y_0)$ | Rearranging |
| $$h’=v_4=(\frac{L_1+L_2+L_3}{L_1})(-v_0)$ | Derivative wrt. time |
| $$v’_4=a_4=(\frac{L_1+L_2+L_3}{L_1})(-a_0)$ | Derivative wrt. time |
Generalizing for n stages:
| Equation | Comment |
|---|---|
| $$a_{n+1}=(\frac{L_1+L_2+L_3+L_n}{L_1})(-a_0)$$ |
If object 0 was replaced by a winch, find the Torque needed to move the elevator in terms of $a_4$ and other variables. Assume the winch has a constant spool radius $r$.
| Equation | Comment |
|---|---|
| $$T_3=m_4a_4+W_4=m_4a_4+m_4g$$ | Net force eq. for Obj. 4 |
| $$T_3=m_4(a_4+g)$$ | |
| $$T_2=m_3(a_3+g)+2T_3$$ | Similar to finding $a$ in static equilibrium |
| $$T_1=m_2(a_2+g)+2T_2$$ | |
| $$F=T_1$$ | |
| $$F=m_2(a_2+g)+2T_3$$ | |
| $$F=m_2(a_2+g)+2m_3(a_3+g)+4T_3$$ | |
| $$F=m_2(a_2+g)+2m_3(a_3+g)+4m_4(a_4+g)$$ | |
| $$a_4=(\frac{L_1+L_2+L_3}{L_1})(-a_0)$$ | Answer from previous section |
| $$a_0=\frac{-a_4L_1}{L_1+L_2+L_3}$$ | |
| $$a_2=-a_0$$ | |
| $$a_2=\frac{a_4L_1}{L_1+L_2+L_3}$$ | Substitution |
| $$a_3=(\frac{L_1+L_2}{L_1})(\frac{a_4L_1}{L_1+L_2+L_3})$$ | |
| $$a_3=a_4(\frac{L_1+L_2}{L_1+L_2+L_3})$$ | Simplification |
| $$F=m_2(a_4(\frac{L_1}{L_1+L_2+L_3})+g)+2m_3(a_4(\frac{L_1+L_2}{L_1+L_2+L_3})+g)+4m_4(a_4+g)$$ | |
| $$\tau=Fr=m_2r(a_4(\frac{L_1}{L_1+L_2+L_3})+g)+2m_3r(a_4(\frac{L_1+L_2}{L_1+L_2+L_3})+g)+4m_4r(a_4+g)$$ |
Generalizing for n stages:
$$\tau=m_2r(a_{n+1}(\frac{L_1}{L_1+L_2+L_n})+g)+2m_3r(a_{n+1}(\frac{L_1+L_2}{L_1+L_2+L_n})+g)+2^{n-1}m_{n+1}r(a_{n+1}(\frac{L_1+L_2+L_m}{L_1+L_2+L_n})+g)$$