Partial Derivatives

Intro

Partial derivatives are a simple yet powerful technique for evaluating how multivariate function change with respect to a certain variable.

Concepts

Partial Derivatives
Chain Rule/ Implicit Differentiation

Partial Derivatives

Relevance: This section reveals how to take simple partial derivatives and some applications in FRC.

For a function, y(x), standard derivatives are notated as:

$$\frac{dy}{dx}=\frac{d}{dx}y$$

For a function, f(x, y), partial derivatives are notated as:

$$f_x=\frac{\partial f}{\partial x}=\frac{\partial}{\partial x}f$$

$$ f_x \text{ and variations are pronounced as the partial derivative of f with respect to x. Since f was a function of x and y, f has two first order partials: } f_x \text{ and } f_y. $$

Partials are computed by holding all variables constant and only treating the variable we are taking the derivative of as a variable.

Let us do an example:

$$ \text{For the function } f(x, y) = x^2 + y^3 \text{, find all first order partials.} $$

$$f_x = 2x$$

$$ \text{When we take the derivative of } x^2 + y^3 \text{, y is a constant and the derivative of a constant is 0 so that term disappears.} $$

$$f_y = 3y^2$$

An example relevant to FRC would be to find out wether changing the size of the base sprocket or the wrist sprocket of a weighted four bar would be more effective at increasing the angle the wrist makes with the arm.

The formula for a weighted four bar is:

$$\Delta \theta_\frac{wrist}{arm}=\frac{r_{base}}{r_{wrist}}\Delta \theta_{base}$$

Rewritten in an easier to manipulate format:

$$f=\frac{r_1}{r_2}\theta$$

Finding the relevant partials:

$$f_{r_1}=\frac{\theta}{r_2}$$ $$f_{r_2}=-\frac{r_1\theta}{r_2^2}$$

So what does this tell us? $$ f_{r_1} \text{ tells us that increasing the base sprocket will increase the wrist to arm angle by a factor of } \frac{\theta}{r_2}. $$

$$ f_{r_2} \text{ tells us that decreasing the wrist sprocket will increase the wrist to arm angle by a factor of } \frac{r_1\theta}{r_2^2}. $$

$$ \text{Changing the base sprocket will increase the wrist to arm angle more than decreasing the wrist sprocket if } f_{r_1} > -f_{r_2}. $$

$$\frac{\theta}{r_2} > \frac{r_1\theta}{r_2^2}$$ $$r_2>r_1$$

Finally, we can conclude that increasing the base sprocket will increase the wrist to arm angle faster if the wrist sprocket is larger than the base sprocket. Otherwise, when the wrist sprocket is smaller than the base sprocket, decreasing the wrist sprocket will increase the wrist to arm angle faster.

Chain Rule

Relevance: The multivariate chain rule allows one to find the rate of change of nested functions much like the univariate chain rule.

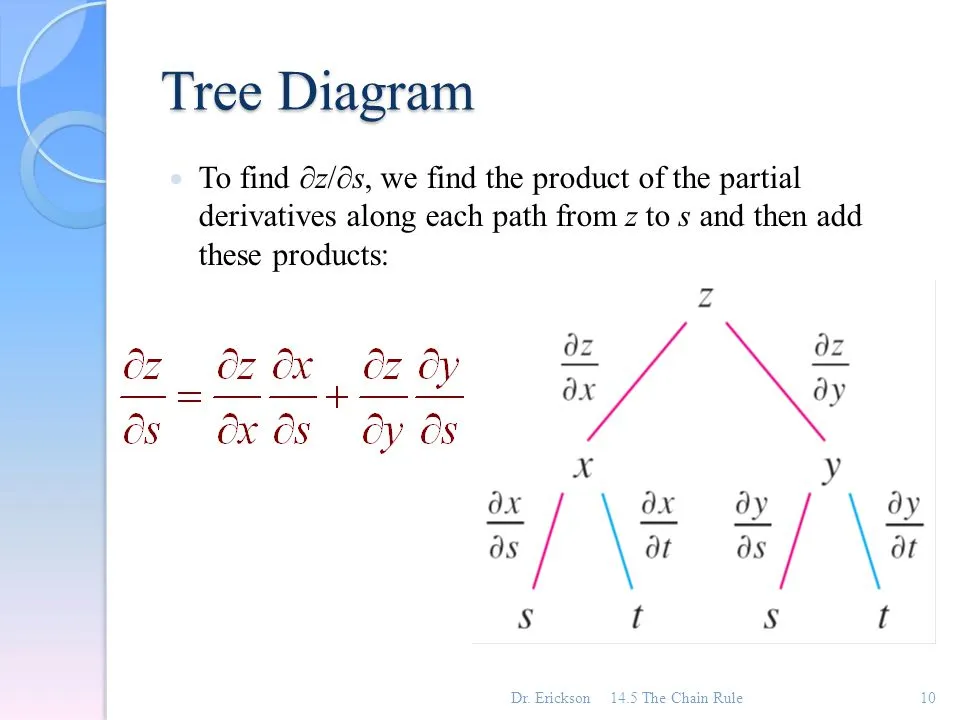
$$ \text{The above diagram shows a function z that is a function of x and y which are both functions of s and t: } z=f(x(s, t), y(s, t)). $$

An example:

$$z=x^2+y^2$$ $$x=s^2$$ $$y=2st$$

Finding the partials: Finding $z_s$:

$$z_s=\frac{\partial z}{\partial x}\frac{\partial x}{\partial s} + \frac{\partial z}{\partial y}\frac{\partial y}{\partial s}$$ $$z_s=(2x)(2s)+(2y)(2t)$$ $$z_s=4xs+4yt$$

Finding $z_t$:

$$z_t=\frac{\partial z}{\partial x}\frac{\partial x}{\partial t} + \frac{\partial z}{\partial y}\frac{\partial y}{\partial t}$$ $$z_t=(2x)(0)+(2y)(2s)$$ $$z_t=4ys$$

Continuing off of our previous FRC example, we have our weighted four bar but let’s say we want to determine if changing the size of the wrist or base sprocket will increase the wrist to ground angle.

The formula for a weighted four bar is:

$$\Delta \theta_\frac{wrist}{arm}=\frac{r_{base}}{r_{wrist}}\Delta \theta_{base}$$

$$\Delta \theta_\frac{wrist}{ground}=\Delta \theta_{base}-\Delta \theta_\frac{wrist}{arm}$$

Rewritten in an easier to manipulate format:

$$\theta_2=\frac{r_1}{r_2}\theta_1$$

$$\theta_3=\theta_1-\theta_2$$

Finding the relevant partials:

$$\theta_{3_{r_1}}=\frac{\partial \theta_3}{\partial \theta_2}\frac{\partial \theta_2}{\partial r_1}$$

$$\theta_{3_{r_2}}=\frac{\partial \theta_3}{\partial \theta_2}\frac{\partial \theta_2}{\partial r_2}$$

$$\frac{\partial \theta_3}{\partial \theta_2}=-1$$

The other partials that are needed to find $\theta_{3_{r_1}}$ and $\theta_{3_{r_2}}$ were found in the previous section with different variable names. It is reproduced below with the corresponding variables names.

$$\frac{\partial \theta_2}{\partial r_1}=\frac{\theta_1}{r_2}$$ $$\frac{\partial \theta_2}{\partial r_2}=-\frac{r_1\theta_1}{r_2^2}$$

Thus,

$$\theta_{3_{r_1}}=-\frac{\theta_1}{r_2}$$ $$\theta_{3_{r_2}}=\frac{r_1\theta_1}{r_2^2}$$

Following very similar steps to the FRC example in the previous section:

$$-\frac{\theta_1}{r_2}>-\frac{r_1\theta_1}{r_2^2}$$ $$r_2<r_1$$

We can conclude that increasing the base sprocket will increase the wrist to ground angle faster if the wrist sprocket is smaller than the base sprocket. Otherwise, when the wrist sprocket is larger than the base sprocket, decreasing the wrist sprocket will increase the wrist to ground angle faster.